1. P2: Sample Space and Assigning Probabilities TOPIC P2: Sample Space and Assigning Probabilities Spotlight: The Casino Game of Roulette. Roulette is one of the most popular casino games. The name roulette is derived from the French word meaning small wheel.
2. PROBABILITY OF SUCCESS = Ways to Win / Ways to Win + Ways to Lose. Probability always belongs within the range between 0 and 1 and can be expressed as a fraction or a decimal. If one is to present probability as a percentage, then the decimal needs to be multiplied by 100. Let us use a simple example of tossing a coin.
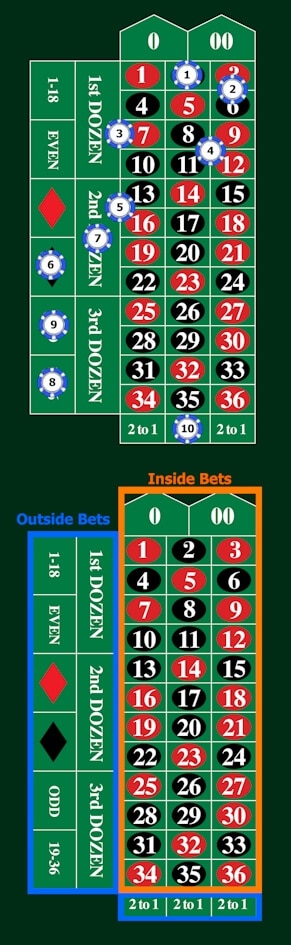
3. An American roulette wheel contains 38 slots: 18 red, 18 black, and 2 green. A casino has purchased a new wheel and they want to know if there is any evidence that the wheel is unfair. They spin the wheel 100 times and it lands on red 44 times, black 49 times, and green 7 times.

Which outcome has a higher probability after eight successive Blacks, Black again or Red? Probability, the Martingale system and the 'delayed' double-up betting strategy. At roulette each spin is a new spin and the outcome is never determined by prior spins. After eight successive blacks, a black is as likely to come up as a red.

You hear people talk about “odds” and “probabilities” all the time. You might have wondered if these words mean the same thing or if they have different meanings.

The answer to your questions is “yes” (and “no”).

American English is often described as a “lazy” language because no matter how precise a meaning you intend for any newly devised word, sooner or later someone will use that word in an unexpected way.

The English language has developed a huge selection of synonyms, words with the same or nearly same meaning, for many different concepts. “Odds” and “probabilities” can be synonymous and in common usage often are.

But even in gambling circles you’ll find people using either word with a precise meaning that is not intended to be synonymous with the use of the other word.

In other words, it’s okay to say either “odds” or “probabilities” in most situations. Use whichever word you prefer; most people will understand your meaning.

But as you learn more about gambling and statistics you’ll recognize those special cases where each word means something different from the other one.

This post explains the differences for you in (hopefully) plain, simple language.

Let’s begin with simple definitions for these words:

What Are the Definitions for “Odds” and “Probability?”

Odds – The primary definition given for this word is about the “ratio between two amounts staked by parties to a bet”. This technical definition can be and often is clarified. Here’s an example:

The odds in roulette are typically different from the odds in craps. The reason for these differences is that each game has different expected probabilities. A bet on a single number in roulette pays off at 35 to 1 odds, but the odds of winning are 37 to 1. A bet on a specific number in craps has different odds depending on which number you’re choosing. The payoff odds for those bets vary, too.

Probability – The usual definitions given for this word are confusing because they use the word “probable”. An example definition might read: “the extent to which something is probable; the likelihood of something happening or being the case.”

That’s okay when you’re speaking casually.

But there’s a more precise meaning for probability in the field of statistics. It’s important to understand the statistics definition for this word because many gambling tutorials and experts draw upon statistics to explain probabilities in games of chance.

How Is Probability Computed in Statistics?

In statistics a probability is derived from the distribution of a set of scores. The distribution is the set of all the values that have been collected from some type of operation. The set could consist of all possible values resulting from the operation OR the set could consist of all recorded values resulting from execution of the operation more than once. That might be a little confusing.

So let’s look at a classic statistics example: a simple coin toss.

A coin has two sides (we ignore the edge of the coin). When you toss a coin it will land either HEADS facing up or TAILS facing up (again, we ignore any case where it lands on the edge). This gives us a probability set of 2 items: HEADS and TAILS. We say, based on the number of items in this 2-item set, that both HEADS and TAILS have a 0.50 (or 50%) probability of turning up as a result of the coin toss. Both outcomes are equally likely.

But suppose you want to test that probability. You might toss the coin in the air 100 times. You could also write a computer program to simulate a coin toss and use it to run 1,000,000 simulations. In this example, you record the outcomes of the simulations or real coin tosses and tally up how many times the coin lands HEADS up and TAILS up. In practice you might not find an exact 50% split between the two possible values. These recorded outcomes are the SCORES in your PROBABILITY DISTRIBUTION.

In short, “probability” could refer to either the EXPECTED OUTCOME based on the number of possible outcomes.

OR it could refer to the subset of outcomes of a specific score from a set of real outcomes collected from an experiment or data source.

This distinction is important because it will help you understand the limitations of calculating probabilities for gambling games.

How Are Odds Computed for Gambling Games?

Casinos rely on “odds” to determine how much they will pay players who win their games. The odds are calculated so that, over a long period of time, the casinos will retain a certain expected percentage of the players’ wagers. This is where casinos get their income. The players’ winnings are paid out of the total sum of the wagers they place.

In other words, if a gambling game has a probability of 1% of producing a specific result, the casino may pay a player $99 when that result occurs. The $99 is retained from other player wagers. The player who wagered the winning $1 loses his wager but is awarded $99. Or you could say the player wins $98 and keeps his $1 wager. The casino’s $1 profit is called the “house edge”.

Of course, the money really passes back and forth continuously as players make bets. Players win some bets, and they lose some bets. All the casino cares about is that it retains a small percentage of the bets over time.

But each game is designed to retain a different expected percentage. The “odds” for a game are computed to ensure the casino gets its percentage. Here’s an example using roulette:

You’ll find 3 styles of roulette available in the United States today:

1. European Roulette
2. American Roulette
3. Sands Roulette.

The chief difference between these games is found on the roulette wheel:

The European wheel has exactly 18 black slots, 18 red slots, and 1 green slot.

The American wheel has 18 black slots, 18 red slots, and 2 green slots.

And the Sands wheel has 18 black slots, 18 red slots, and 3 green slots.

All things being considered equal, the probability of the roulette ball landing on any number is 1 divided by ( 18 + 18 + number of green slots). In American Roulette the probability works out to 1 / 38 (or about 0.026, aka “2.6%”).

Notice, too, that the probability would be different for the other 2 versions of the game. Each game has a different total number of slots. So the probability on a European wheel is 1 /37, and the probability on the Sands wheel is 1 /39.

But if you place a bet on any specific number and the ball lands on that number’s corresponding slot, you’ll only be paid a prize of 35 times your bet. That’s true regardless of which game you play. The difference between the payoff odds and the odds of the bet winning is where the house edge stems from.

In other words, the casino has shaved off a little bit of the probability so that it makes a slight profit on the odds. The probability is what is likely to happen but the odds are what you are paid.

How Reliable Are Probability Simulations?

If you research gambling games you’ll find that people have calculated some impressive probability tables for virtually all the major games. These probability tables may be based on millions, even billions of iterations (repeated simulations). They’re considered reliable in establishing expected outcomes, but they don’t predict what’s going to happen in a specific game. We use these probability tables to estimate what is safe to bet on a specific situation, such as the cards in a hand of blackjack or poker, or the available numbers on a roulette table.

But there are two inherent flaws in relying on probability tables.

First, these results are based on computer random number generators. While random number generators are good they’re not perfect. We don’t yet have true random number generation.

In real life events are random, so there is a slight bias in all probability tables.

Second, any probability distribution–regardless of whether it is based on simulations or real game play–only represents the past. In other words, because future events are truly randomized no probability table can accurately predict the percentage of possible outcomes for any length of play.

In other words, not only is the casino risking NOT retaining as much money as it expects from player wagers, you might play 100 losing hands in a row, or make 1,000 unrewarding slot spins in a row. However unlikely these events may seem to be, they can happen. Probability tables won’t tell you when these least likely series of outcomes will happen. At best a sophisticated probability table will tell you that these unfortunate losing runs are mathematically possible.

Nonetheless, even though a probability table won’t reveal the future to you, it’s better to consult these tables when deciding how you’re going to bet your money. Experienced gamblers have learned to fold their cards in certain situations because the chances of winning are far outweighed by the chances of losing. Experienced roulette players may make more conservative wagers than inexperienced players because they know their chances of winning are better with the conservative wagers.

Odds and Probabilities Tell Us One Important Thing about Gambling

Both odds and probability tell us something important about casino gambling:

The house always wins.

The longer you play, the more of your money the house will keep.That’s just how the math works.

Blackjack Probability Example

So why do people keep gambling?

For one thing, taking any kind of risk can be fun. People enjoy taking risks. And given that only about 10% of the population are prone to become addicted to gambling, most people can safely gamble for a few hours a night and still use good judgment. Of course, if you’re drinking or doing drugs and gambling your judgment will be impaired.

But we gamble because it’s fun–not because we’re probably going to win.

Roulette Wheel Probability

That being said, professional gamblers not only enjoy the game but count on it for an income.These pros find ways to take advantage of inherent conditions in the game which can provide them with a mathematical edge over the house. The classic example is someone who counts cards in blackjack, but poker pros and sharp sports bettors can also tilt the odds in their favor.

Probability Roulette Wheel Math

If you can stay in the game long enough, even a slot machine game, there is always a chance you’ll win a big prize or pot and get your money back. You may even come out ahead. This happens often enough that people remain interested in gambling. But remember that the probabilities are against you. The players who win are being paid from your wagers. When you win you are being paid from other players’ wagers. That is where the money comes from.

Conclusion

American Roulette Probability

This is why gambling experts caution people not to expect too much from their tips and teachings. It’s great when you win big money but you should look at gambling as a form of entertainment. It’s a way to pass an evening, especially if you’re with friends. The odds will never be in your favor but maybe, just maybe, once in a while you’ll have a really good evening.

Probability Of Winning Roulette

That’s what we all hope for.